Chapter 8
Analysing your Cube

8.1 Smoothing your data

Frequency or velocity smoothing is performed using Kappa:block. It uses a rectangular box filter with each output pixel either the mean or the median of the input pixels within the filter box. The box size can be set to 1 for dimensions which do not require smoothing. In the example below the spatial pixels remain untouched while the velocity axis is smoothed using a box of five channels.

Two-dimensional NDFs can also be smoothed using gausmooth. This smooths using a symmetrical Gaussian point spread function (PSF) of specified width(s) and orientation. Each output pixel is the PSF-weighted mean of the input pixels within the filter box.

Note that the fwhm option is given in the number of pixels. For example, to smooth a map with 4′′pixels by a 12′′Gaussian you would set fwhm=3.

8.2 Removing a baseline

Baselines can be removed using Kappa:mfittrend. This routine can fit polynomials up to order 15, or cubic splines, to each spectrum in your cube. You can specify the ranges to fit via the ranges parameter, or you can allow them to be determined automatically (auto), say if the number of observations is large.

If using automatic range determination you should set the numbin option. This is the number of bins in which to compress the trend line. A single line or average may be noisy so binning is used to improve the signal-to-noise in order to enhance features that should be masked.

Ideally the bin size should match your line width to get maximum single to noise between the emission and the background. Be aware that bins that are too big can dilute weaker features. Likewise, bins that are too small will get noisy at the edges of broad lines. We recommend you experiment with the bin size to find the best fit for your data.

To exclude features that are not part of the baseline trend you can use the clip option. Use clip to provide an array of standard deviations for progressive clipping of outliers within each bin. Once the data have been binned a trend is fit within each bin and the outliers clipped, the trend is then re-fitted and the outliers again clipped etc. By default this will clip at 2, 2, 2.5 and 3 $\sigma$ successively but you may wish to experiment with your own clip levels. The clip option is only used when auto=true.

For convenience Gaia has a Baseline tab in its cube control panel—see Section 10.1 for an example. This invokes mfittrend.

8.2.1 Advanced method

These steps give a more in depth way of determining the baselines and mimic the pipeline.

(1)

Perform a block smooth on your reduced cube. Here the smoothing is quite aggressive with a box filter of five pixels along the spatial axes and fifteen pixels along the frequency axis. This is to really pull out all emission features. You can tweak these to suit your data, e.g a narrower box might be needed if you have very narrow lines.

  % block in=cube out=temp1 box="[5,5,15]" estimator=mean

(2)

Perform mfittrend on your smoothed cube with a high-order polynomial and automatic range determination.

  % mfittrend in=temp1 out=temp2 axis=3 order=3 auto method=single \
    variance subtract=false mask=blmask

(3)

Add the baseline mask to your original unsmoothed cube.

  % add in1=cube in2=blmask out=temp3

(4)

Perform mfittrend on your masked unsmoothed cube with a lower-order polynomial. This time fit the full range by setting auto=false.

  % mfittrend in=temp3 out=temp4 axis=3 order=1 auto=false ranges=\! \
    method=single variance=true subtract=false

(5)

Subtract the baseline from the original unsmoothed cube.

  % sub in1=cube in2=temp4 out=baselinedcube

8.2.2 What about findback?

The Cupid routine findback offers an alternative for background subtraction however there are more limitations. It applies spatial filtering to remove structure with a size scale less than a specified box size. Within each box the values are replaced by the minimum of the input values. The data are then filtered again and this time replaced with the maximum in each box.

Using findback results in a baseline trend that hugs the lower limit of the noise and can contain sharp edges. These problems can be mitigated but extra steps are required. See SUN/255 for more details.

8.3 Collapsing your map

An integrated intensity map can be created by collapsing your cube along the frequency/velocity axis using Kappa:collapse. For each output pixel, all input pixels between the specified bounds are collapsed and combined using one of a selection of estimators. Amongst others, the estimators include the mean, integrated value, maximum value, the mean weighted by the variance, RMS value and total value. See SUN/95 for a full list.

The example below includes the options low and high which can be specified to limit the range over which the cube is collapsed on the given axis (in this case from $-5$ km s$-1$ to $+10$ km s$-1$). The variance flag indicates the variance array should be used to define weights and generate an output variance. The option wlim sets the fraction of pixels that must be ‘good’ in the collapse range for a valid output pixel to be generated. You may find you need to reduce the value for wlim below its default of 0.3 for some data.

If you do not know the axis name you can give the number instead (1=RA, 2=Dec, 3=vrad).

For convenience Gaia has a Collapse tab in its cube control panel—see Section 10.6 for an example. This invokes collapse.

8.3.1 Advanced method

These steps mimic the pipeline and show the procedure for generating an integrated map collapsed only over regions with emission greater than 3 $\sigma$.

(1)

Use findclumps to run a clump-finding algorithm on your cube. Specify the 3 $\sigma$ limit in your configuration file. See Section 9.5 for more details on clump-finding and Section 8.9 for how to determine your RMS.

  % findclumps in=cube rms=<medianrms> config=^myconfig.dat \
    method=clumpfind out=temp1 outcat=mycat deconv=no

(2)

Divide the map by itself to create a clump mask that has clump regions set to 1.

  % div in1=temp1 in2=temp1 out=temp2

(3)

Set the bad data to zero using Kappa:nomagic.

  % nomagic in=temp2 out=temp3 repval=0

(4)

Multiply your reduced cube by the clump mask.

  % mult in1=cube in2=temp3 out=maskedcube

(5)

Collapse your masked reduced cube.

  % collapse in=maskedcube out=integ estimator=integ wlim=0.1 variance

8.3.2 Moments maps

You can use collapse to generate the moments maps by selecting the appropriate estimator option—Integrated value (Integ) for the integrated map (zeroth moment), Intensity-weighted co-ordinate (Iwc) to get the velocity field (first moment), or Intensity-weighted dispersion (Iwd) to get the velocity dispersion (second moment).

8.4 Temperature scales

Your cube will come out of makecube and the pipeline, in units of $T_{\text{A}}^{\ast }$. To convert this to main-beam brightness temperature, $T_{\text{MB}}$ divide your cube by the main-beam efficiency, ${\eta }_{\text{MB}}$. Alternatively, to convert to corrected radiation temperature, $T_{\text{R}}^{\ast }$, divide by the forward scattering and spillover efficiency, ${\eta }_{\text{ fss}}$. See Section 3.2 for efficiency values for RxA and HARP, and the JCMT webpages for further information and historical numbers.

You can use the Kappa command cdiv to divide any NDF by a constant.

8.5 Changing the pixel size

You may want to regrid your data onto larger pixels, for instance to allow direct comparison with data from other observatories. In the example below a JCMT map is regridded and aligned to match a Herschel map. See Appendix B for instructions on converting your FITS file to NDF format.

Alternatively, to resample your data onto smaller pixels you should use the Kappa command sqorst. In the example below ’map’ has a pixel size of 8′′, while ‘resamplemap’ has a pixel size of 4′′– the number of pixels has been doubled by applying a factor of 2 to the spatial axes. A factor of 1 was applied to the frequency (third) axis leaving it unchanged.

mode=factors is the default setting so it was not specified in the example above. The example below however, uses mode=pixelscale to define a pixel size for the third axis; here the spectra are rebinned into 2 km s$-1$ channels.

Remember you can check your current pixel size and channel spacing with ndftrace (see Section 2.4).

8.6 Mosaicking cubes

If you pass raw files covering different regions of the sky to makecube it will automatically mosaic them together. This can be heavy work for your processor so you may wish to make individual cubes and combine them during post-processing. To co-add multiple reduced maps you should use wcsmosaic.

Note that this is not the same as stitching the tiles of a reduced cube from a single makecube command. Such tiles share common pixel co-ordinates and so can be combined with paste (Section 6.6.1). Separately created cubes will not have the same pixel co-ordinates, and therefore the world co-ordinates are required to align the tesserae in the mosaic of an extended region.

By selecting the lower bound (lbnd) and upper bound (ubnd) to be default (!) you are including all of the input tiles. You can change these if you want to only mosaic a sub-region of the input maps. As with makecube there are a number of regridding options available to you describing how to divide an input pixel between a group of neighbouring output ones (the default is SincSinc).

Note that by default wcsmosaic aligns reduced cubes along the spectral axis using the heliocentric standard of rest (the Orac-dr pipeline also does this). If you want to align using a non-heliocentric standard of rest, you should set the AlignStdOfRest attribute for your NDFs using wcsattrib before running wcsmosaic. The following example sets the alignment to the kinematic LSR.

where $<$list_of_separate_cubes$>$ is group of cubes specified as a comma-separated list or as one per line in a text file.

8.7 Cropping your map

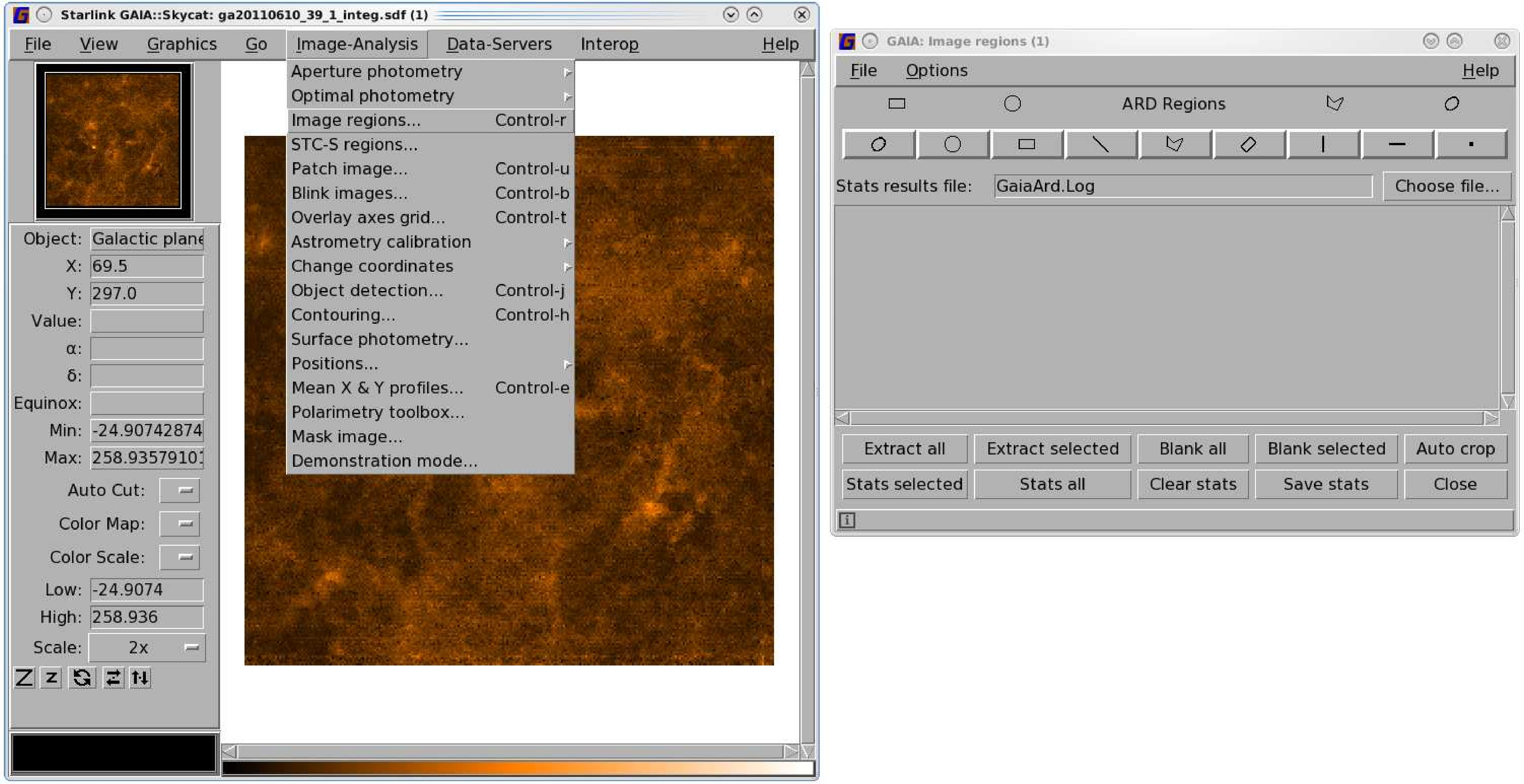
Cropping an ACSIS map can be fiddly. The simplest way is to create an ARD mask in Gaia and apply it to your map. The steps below work on both two- and three-dimensional data.

(1)

Create your ARD mask. You may find it easiest to do this with Gaia. See Figure 8.2 for an illustrated guide.

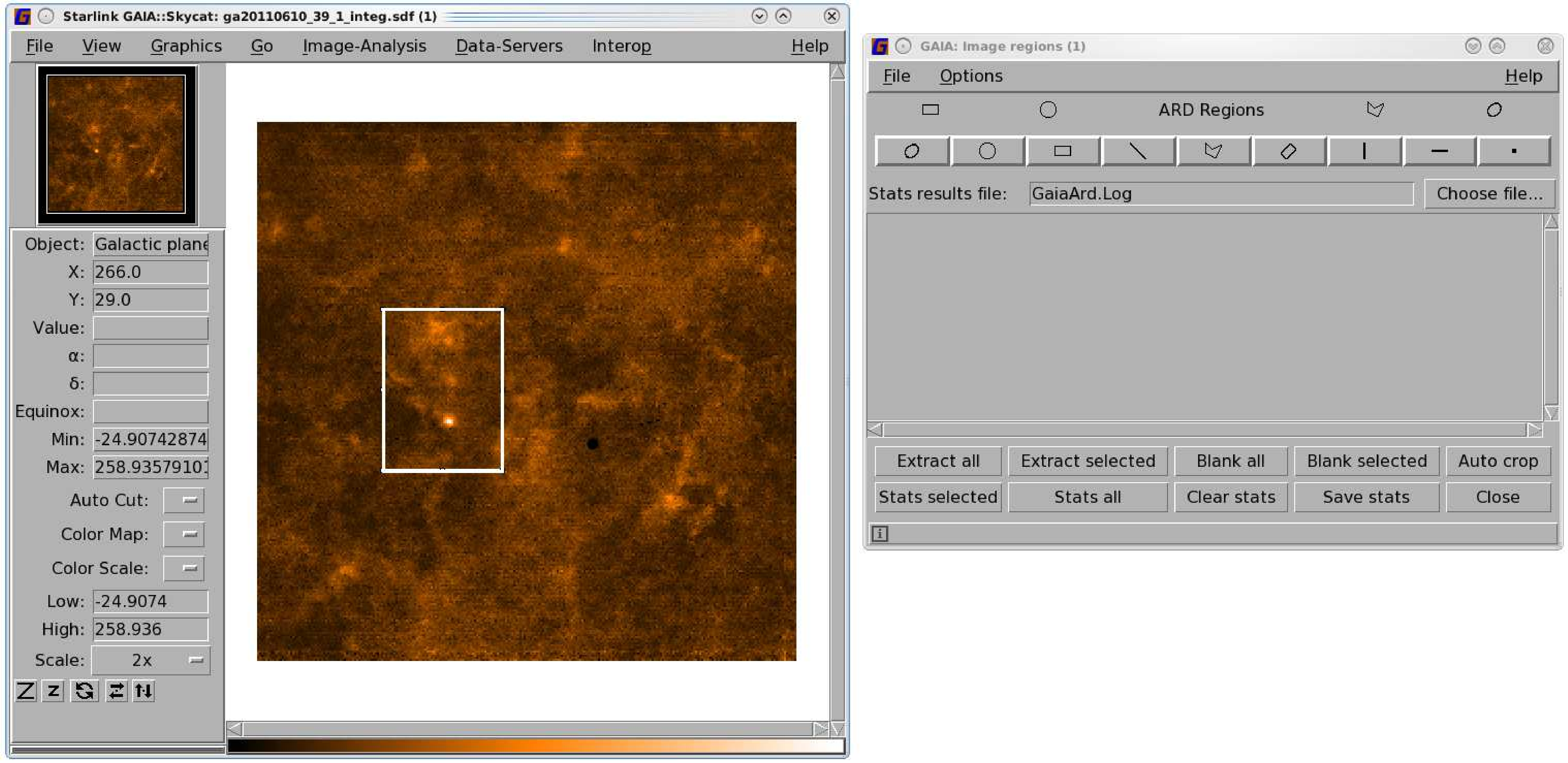
(2)

Trim off the third axis from your mask using ndfcopy.

  % ndfcopy mask trim trimwcs

(3)

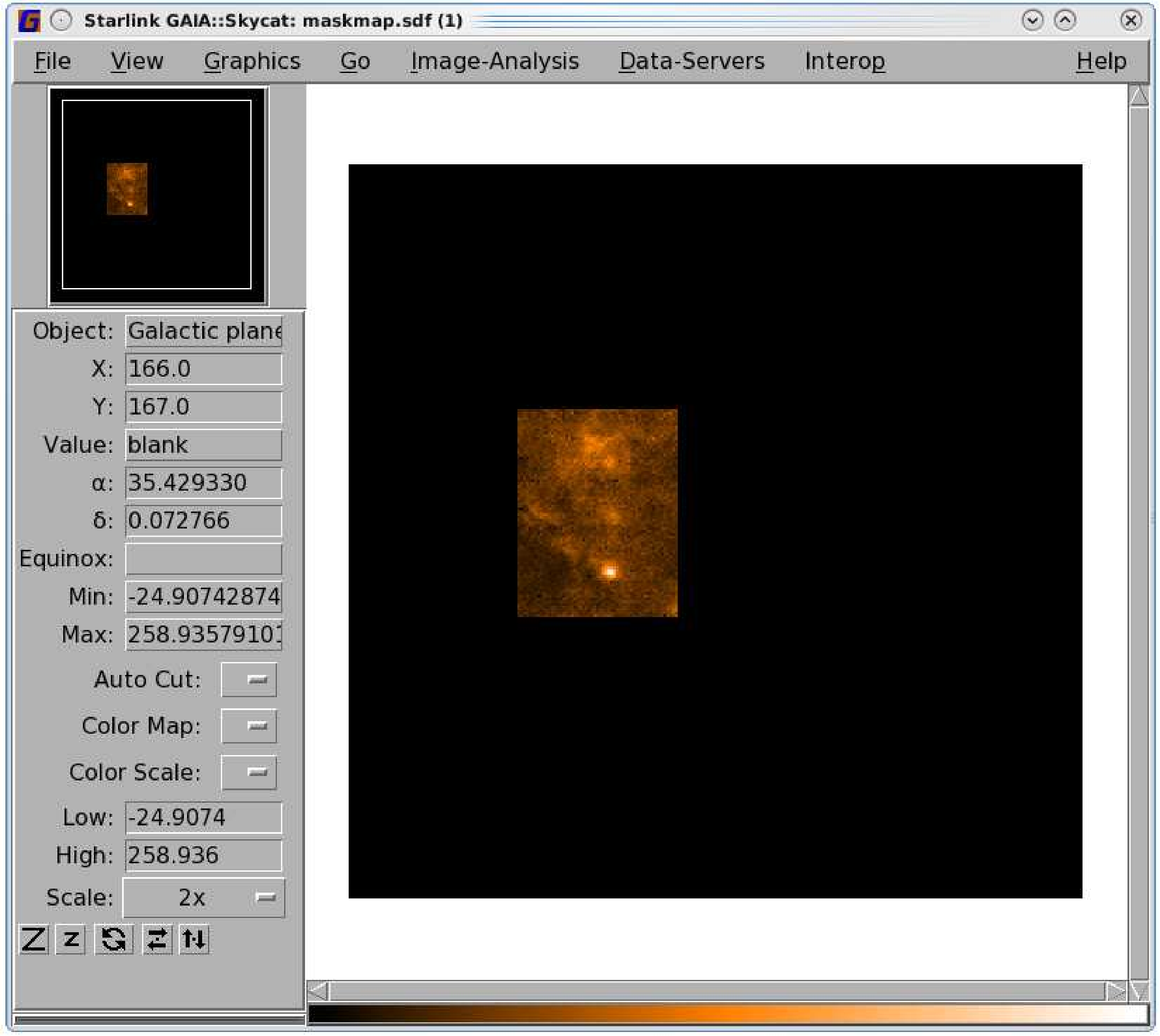
Apply the saved ARD mask to your map. Setting inside=false will mask the pixels outside rather than inside your mask. The masked pixels will appear blank when you open it with Gaia; see the left-hand panel of Figure 8.2.

  % ardmask map inside=false ard=ardmask.txt out=maskmap

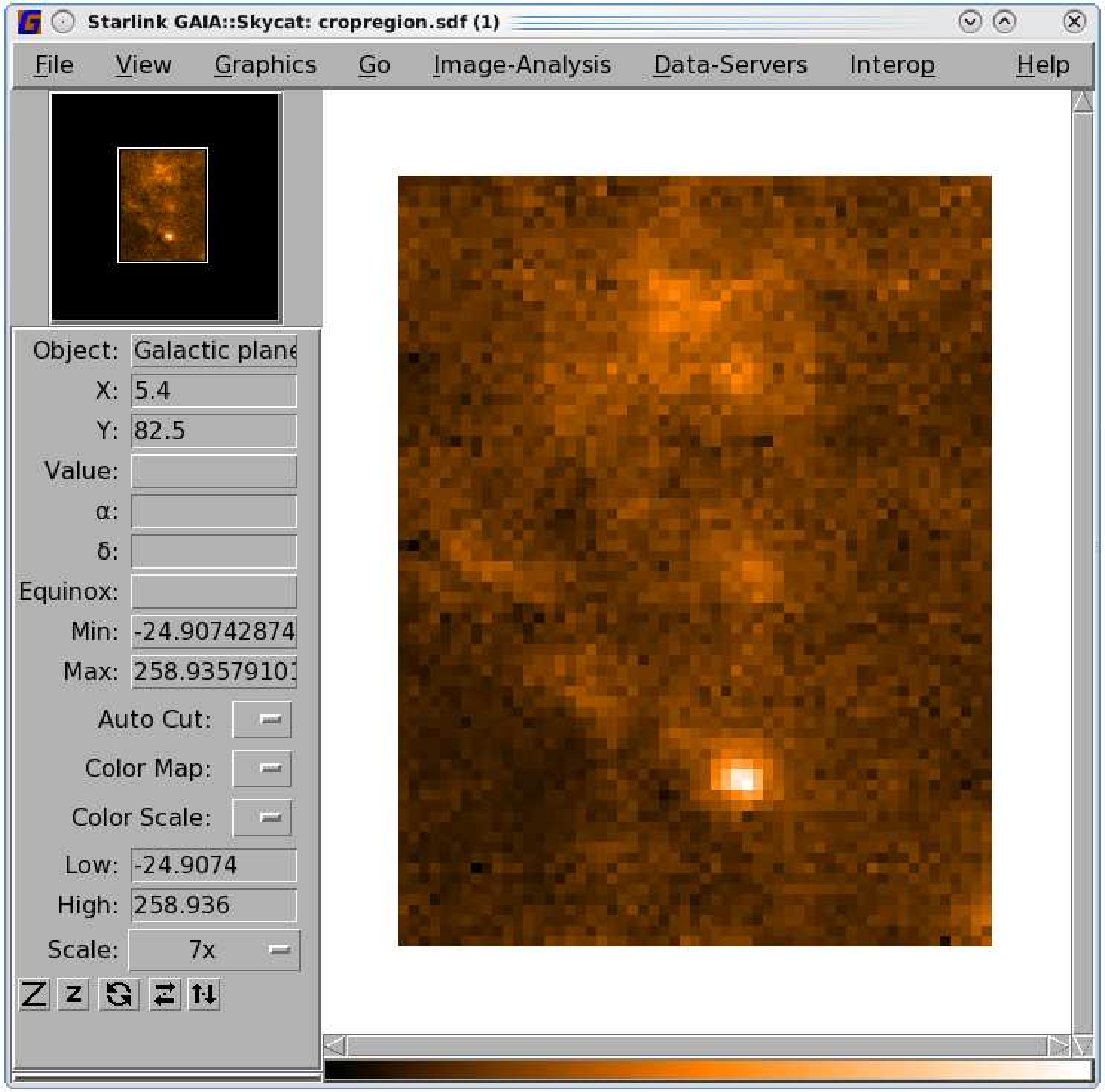
(4)

Trim off the blank pixels using ndfcopy with the trimbad option. This leaves just your selected region; see the right-hand panel of Figure 8.2.

  % ndfcopy maskmap trimbad

An alternative method is to use ndfcopy while defining the section of the map or cube you wish to extract as an output cube. See Section 2.6.

8.7.1 Supplying a template

If you wish to extract only a region which overlaps with an existing file you have, e.g. from a different observing campaign or telescope, you can also use ndfcopy but with the like option.

The shape of the file supplied by like will determine the shape of the output file. This shape can be in either pixel indices or the current WCS Frame. If the WCS Frame is required, include the parameter likewcs to the command line otherwise it can be omitted.

Figure 8.2: (Left) After applying the ARD mask, the cropped region is still surrounded by blank pixels. (Right) The blank pixels have been trimmed using ndfcopy with the trimbad option.

8.8 Filling holes in your map

You may come across empty pixels in your map due to dead receptors or receptors which have failed quality assurance in the pipeline. The second half of 2013 in particular had only twelve working receptors for HARP.

You can fill these holes using Kappa:fillbad. This replaces the bad values with a smooth function derived from neighbouring values, derived by iterating to a solution of Laplace’s equation.

The default values for fillbad will fill the holes but smooths by five pixels along each axis. If you prefer not to smooth in the spectral axis, set the parameter size to [$s$,$s$,0] where $s$ is the scale length in pixels. The zero means do not smooth along the third axis.

The scale length should have a value about half the size of the largest region of bad data to be replaced. Since the largest bad regions apart from the cube peripheries are two pixels across, a size of 1 is appropriate.

Figure 8.3 shows an initial map with holes and the final filled map.

Figure 8.3: Filling holes in your HARP map with fillbad. Compare the original map (left) with the filled map (right). A blue pixel indicates an undefined spectrum.

8.9 Checking the noise

You can use Kappa:stats to check the noise in your map. It will report the statistics for all pixels so be aware that noisy edges and strong signal will contribute to the standard deviation. You can mitigate this by trimming any noisy edges and by examining the square root of the VARIANCE component (hereafter referred to as the error component¹) although bright emission will still increase your noise. You can select the error component with comp=err on the command line.

Including the option order allows the ordered statistics such as the median and percentiles to be reported. Note that percentile options will need to be specified via the percentiles parameter.

8.9.1 Visualising the noise

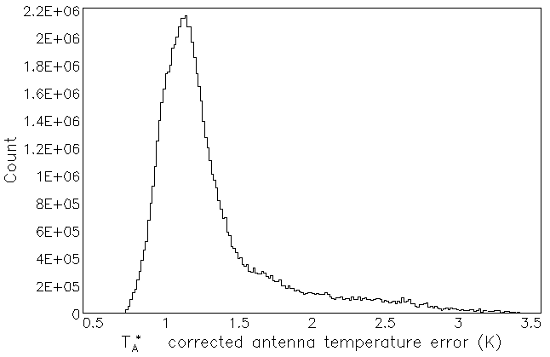
You can plot the noise or error component of your map using the Kappa command histogram. This allows you to visualise the distribution with more ease. Again the comp=err option is used.

The output is shown in Figure 8.4. An alternative to setting the number of bins via the numbin parameter is to set the width of each bin using the width parameter.

Figure 8.4: The error component plotted with histogram.

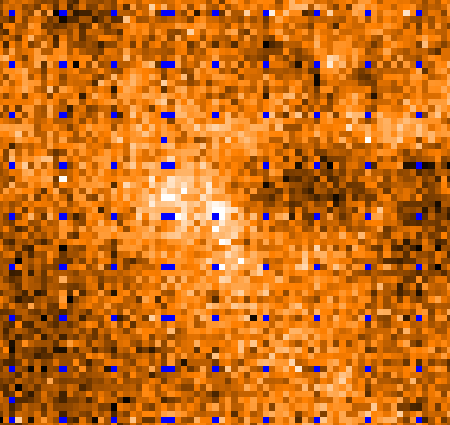
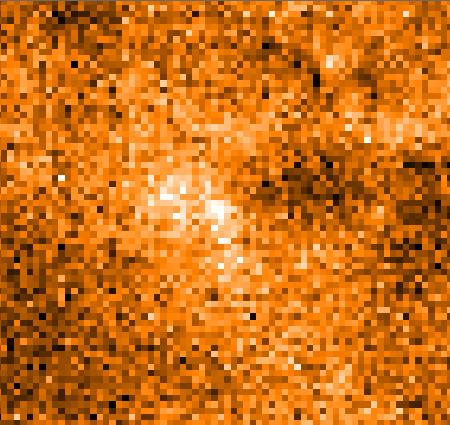
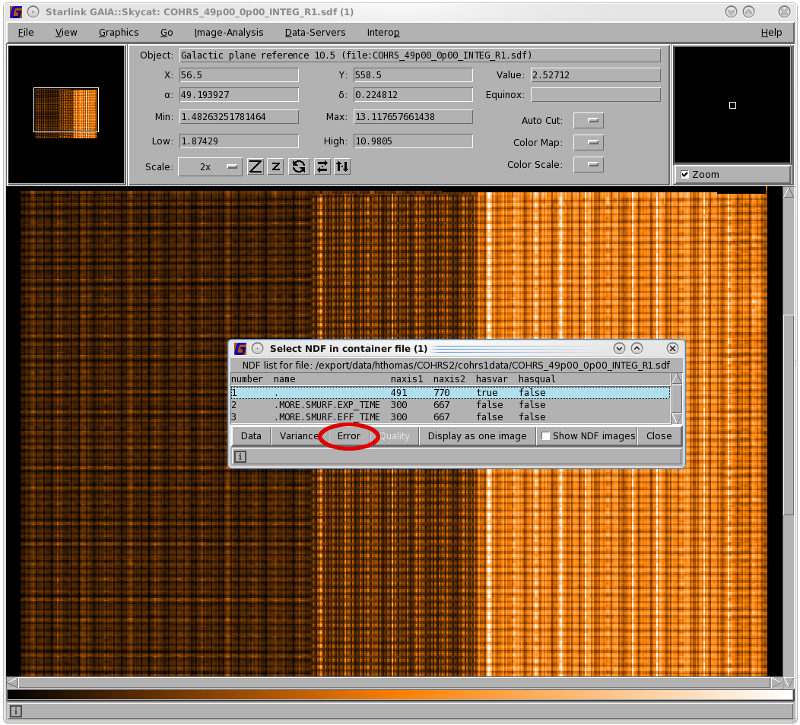
It is also useful to view the noise map itself. Figure 8.5 shows how to select the error component in Gaia. Other options available from the "Select NDF in container file" window include the exposure time, the effective time and, if spread=nearest when running makecube, the system temperature. To return to your main image select the top level and click the Data button.

Figure 8.5: The noise map of a mosaic of tiles taken in differing weather conditions.

8.9.2 HARP flatfielding

The individual detectors in the HARP array do not respond exactly the same to the incoming signal, returning different temperatures for the same flux. If uncorrected, this can lead to artificial net-like patterns in the reduced spectral cube. As with any flatfield correction, the goal is to expose to a uniform source to measure the relative responses of the detectors. However, this is not possible with HARP observations, and the approach is assume that during an observation the detectors see approximately the same signal from the various sources. For extended emission at low galactic latitudes this is a reasonable assumption. For isolated compact sources it is likely to be invalid.

It may be possible to use a flatfield determined on the same night in a high-signal region and apply that to a low-signal or compact-source observation. The flatfield can change during the night, but it might better than no flatfield.

The method of Curtis et al. (2010)[9] creates a map for each detector and integrates the measured flux in the main spectral line. Use the DETECTORS parameter to create a spectral cube from just that detector.

The simplest way to sum the flux across a line run stats over a chosen spectral range, such as $-5$ km s$-1$ to 7.2 km s$-1$.

If there might be bad pixels present, the mean is more accurate than the sum. This assumes that the line is located within these bounds across the whole spatial region. It is wise not to push too far into the wings of the line and baseline errors and noise have a greater impact on the integrated flux.

The receptors are normalised to the flux of the reference receptor, near the centre, normally H05, but given by the FITS header REFRECEP.

There are other methods in Orac-dr, one to cope with multiple lines. It sums all the signal above some threshold, such as the median plus four standard deviations, to exclude the baseline noise. Since the flat ratio biases this sum, Orac-dr iterates to converge to a solution.