We saw in §12 how AST_CONVERT could be used to find a Mapping that inter-relates a pair of coordinate systems represented by Frames. There is a limitation to this, however, in that it can only be applied to coordinate systems that are inter-related by suitable conventions. In the case of celestial coordinates, the relevant conventions are standards set out by the International Astronomical Union, and others, that define what these coordinate systems mean. In practice, however, the relationships between many other coordinate systems are also of practical importance.
Consider, for example, the focal plane of a telescope upon which an image of the sky is falling. We could measure positions in this focal plane in millimetres or, if there were a detector system such as a CCD present, we could count pixels. We could also use celestial coordinates of many different kinds. All of these systems are equivalent in their effectiveness at specifying positions in the focal plane, but some are more convenient than others for particular purposes.
Although we could, in principle, convert between all of these focal plane coordinate systems, there is no pre-defined convention for doing so. This is because the conversions required depend on where the telescope is pointing and how the CCD is mounted in the focal plane. Clearly, knowledge about this cannot be built into the AST library and must be supplied in some other way. Note that this is exactly the same problem as we met in §7.12 when discussing the Domain attribute—i.e. coordinate systems that apply to different physical domains require that extra information be supplied before we can convert between them.
What we need, therefore, is a general way to describe how coordinate systems are inter-related, so that when there is no convention already in place, we can define our own. We can then look forward to converting, say, from pixels into galactic coordinates and vice versa. In AST, the FrameSet class provides this capability.
Consider a coordinate system (call it number 1) which is represented by a Frame of some kind. Now consider a Mapping which, when applied to the coordinates in system 1 yields coordinates in another system, number 2. The Mapping therefore inter-relates coordinate systems 1 and 2.
Now consider a second Mapping which inter-relates system 1 and a further coordinate system, number 3. If we wanted to convert coordinates between systems 2 and 3, we could do so by:
We are not limited to three coordinate systems, of course. In fact, we could continue to introduce any number of further coordinate systems, so long as we have a suitable Mapping for each one which relates it to one of the Frames already present. Continuing in this way, we can build up a network in which Frames are inter-related by Mappings in such a way that there is always a way of converting between any pair of coordinate systems.
The FrameSet (Figure 7) encapsulates these ideas. It is a network composed of Frames and associated Mappings, in which there is always exactly one path, via Mappings, between any pair of Frames. Since we assemble FrameSets ourselves, they can be used to represent any coordinate systems we choose and to set up the particular relationships between them that we want.
Before we can create a FrameSet, we must have a Frame of some kind to put into it, so let’s create a simple one:
We have set this Frame’s Domain attribute (§7.12) to A so that it will be distinct from the others we will be using. We can now create a new FrameSet containing just this Frame, as follows:
So far, however, this Frame isn’t related to any others.
We can now add further Frames to the FrameSet created above (§13.2). To do so, we must supply a new Frame and an associated Mapping that relates it to any of the Frames that are already present (there is only one present so far). To keep the example simple, we will just use a ZoomMap that multiplies coordinates by 10. The required Objects are created as follows:
To add the new Frame into our FrameSet, we use the AST_ADDFRAME routine:
Whenever a Frame is added to a FrameSet, it is assigned an integer index. This index starts with 1 for the initial Frame used to create the FrameSet (§13.2) and increments by one every time a new Frame is added. This index is the primary way of identifying the Frames within a FrameSet.
When a Frame is added, we also have to specify which of the existing ones the new Frame is related to. Here, we chose number 1, the only one present so far, and the new one we added became number 2.
Note that a FrameSet does not make copies of the Frames and Mappings that you insert into it. Instead, it holds pointers to them. This means that if you retain the original pointers to these Objects and alter them, you will indirectly be altering the FrameSet’s contents. You can, of course, always use AST_COPY (§4.12) to make a separate copy of any Object if you need to ensure its independence.
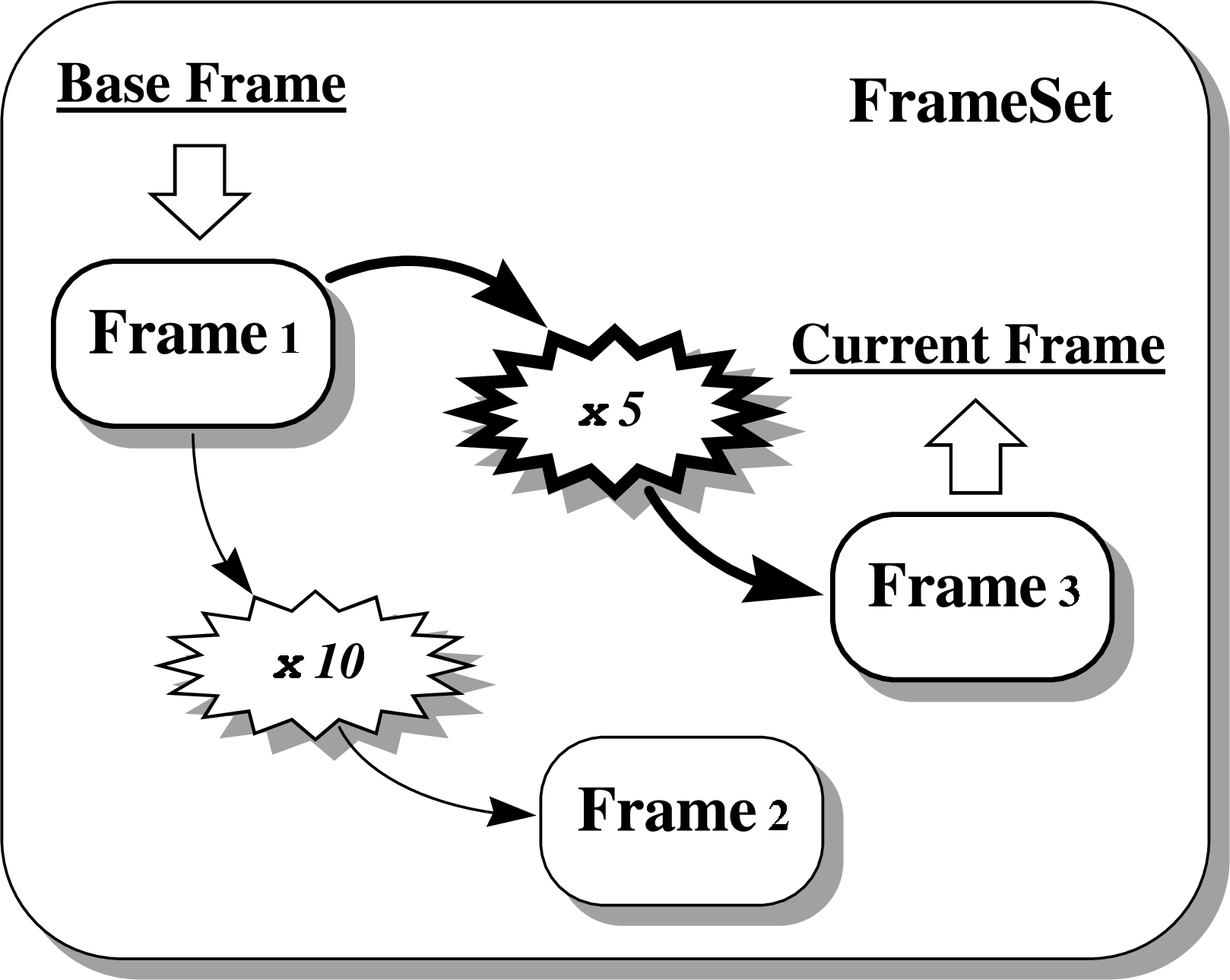
We could also add a third Frame into our FrameSet, this time defining a coordinate system which is reached by multiplying the original coordinates (of FRAME1) by 5:
Here, we have avoided storing unnecessary pointer values by using function invocations directly as arguments for AST_ADDFRAME. This assumes that we are using AST_BEGIN and AST_END (§4.10) to ensure that Objects are correctly deleted when no longer required.
Our example FrameSet now contains three Frames and two Mappings with the arrangement shown in Figure 14.

The total number of Frames is given by its read-only Nframe attribute.
At all times, one of the Frames in a FrameSet is designated to be its base Frame and one to be its current Frame (Figure 14). These Frames are identified by two integer FrameSet attributes, Base and Current, which hold the indices of the nominated Frames within the FrameSet.
The existence of the base and current Frames reflects an important application of FrameSets, which is to attach coordinate systems to entities such as data arrays, data files, plotting surfaces (for graphics), etc. In this context, the base Frame represents the “native” coordinate system of the attached entity—for example, the pixel coordinates of an image or the intrinsic coordinates of a plotting surface. The other Frames within the FrameSet represent alternative coordinate systems which may also be used to refer to positions within that entity. The current Frame represents the particular coordinate system which is currently selected for use. For instance, if an image were being displayed, you would aim to label it with coordinates corresponding to the current Frame. In order to see a different coordinate system, a software user would arrange for a different Frame to be made current.
The choice of base and current Frames may be changed at any time, simply by assigning new values to the FrameSet’s Base and Current attributes. For example, to make the Frame with index 3 become the current Frame, you could use:
You can nominate the same Frame to be both the base and current Frame if you wish.
By default (i.e. if the Base or Current attribute is un-set), the first Frame added to a FrameSet becomes its base Frame and the last one added becomes its current Frame.23 Whenever a new Frame is added to a FrameSet, the Current attribute is modified so that the new Frame becomes the current one. This behaviour is reflected in the state of the example FrameSet in Figure 14.
It is often necessary to refer to the base and current Frames (§13.4) within a FrameSet, but it can be cumbersome having to obtain their indices from the Base and Current attributes on each occasion. To make this easier, two parameter constants, AST__BASE and AST__CURRENT, are defined in the AST_PAR include file and may be used to represent the indices of the base and current Frames respectively. They may be used whenever a Frame index is required.
For example, when adding a new Frame to a FrameSet (§13.3), you could use the following to indicate that the new Frame is related to the existing current Frame, whatever its index happens to be:
Of course, the Frame you added would then become the new current Frame.
The FrameSet class inherits properties and behaviour from the Frame class (§7) and, in turn, from the Mapping class (§5). Its behaviour when used as a Mapping is particularly important.
Consider, for instance, passing a FrameSet pointer to a coordinate transformation routine such as AST_TRAN2:
The coordinate transformation applied by this FrameSet would be the one which converts between its base and current Frames. Using the FrameSet in Figure 14, for example, the coordinates would be multiplied by a factor of 5. If we instead requested the FrameSet’s inverse transformation, we would be transforming from its current Frame to its base Frame, so our example FrameSet would then multiply by a factor of 0.2.
Whenever the choice of base and current Frames changes, the transformations which a FrameSet performs when used as a Mapping also change to reflect this. The Nin and Nout attributes may also change in consequence, because they are determined by the numbers of axes in the FrameSet’s base and current Frames respectively. These numbers need not necessarily be equal, of course.
Like any Mapping, a FrameSet may also be inverted by changing the boolean sense of its Invert attribute, e.g. using AST_INVERT (§5.6). If this is happens, the values of the FrameSet’s Base and Current attributes are interchanged, along with its Nin and Nout attributes, so that its base and current Frames swap places. When used as a Mapping, the FrameSet will therefore perform the inverse transformation to that which it performed previously.
To summarise, a FrameSet may be used exactly like any other Mapping which inter-relates the coordinate systems described by its base and current Frames.
Although it is very convenient to use a FrameSet when a Mapping is required (§13.6), a FrameSet necessarily contains additional information and sometimes this might cause inefficiency or confusion. For example, if you wanted to use a Mapping contained in one FrameSet and insert it into another, it would probably not be efficient to insert the whole of the first FrameSet into the second one, although it would work.
In such a situation, the AST_GETMAPPING function allows you to extract a Mapping from a FrameSet. You do this by specifying the two Frames which the Mapping should inter-relate using their indices within the FrameSet. For example:
would return a pointer to a Mapping that converted between Frames 2 and 3 in the FrameSet. Its inverse transformation would then convert in the opposite direction, i.e. between Frames 3 and 2. Note that this Mapping might not be independent of the Mappings contained within the FrameSet—i.e. they may share sub-Objects—so AST_COPY should be used to make a copy if you need to guarantee independence (§4.12).
Very often, the Mapping returned by AST_GETMAPPING will be a compound Mapping, or CmpMap (§6). This reflects the fact that conversion between the two Frames may need to be done via an intermediate coordinate system so that several stages may be involved. You can, however, easily simplify this Mapping (where this is possible) by using the AST_SIMPLIFY function (§6.7) and this is recommended if you plan to use it for transforming a large amount of data.
A FrameSet can also be used as a Frame, in which capacity it almost always behaves as if its current Frame had been used instead. For example, if you request the Title attribute of a FrameSet using:
the result will be the Title of the current Frame, or a suitable default if the current Frame’s Title attribute is un-set. The same also applies to other attribute operations—i.e. setting, clearing and testing attributes. Most attributes shared by both Frames and FrameSets behave in this way, such as Naxes, Label(axis), Format(axis), etc. There are, however, a few exceptions:
Note that the set of attributes possessed by a FrameSet can vary, depending on the nature of its current Frame. For example, if the current Frame is a SkyFrame (§8), then the FrameSet will acquire an Equinox attribute from it which can be set, enquired, etc. However, if the current Frame is changed to be a basic Frame, which does not have an Equinox attribute, then this attribute will be absent from the FrameSet as well. Any attempt to reference it will then result in an error.
Although a FrameSet may be used in place of its current Frame in most situations, it is sometimes convenient to have direct access to a specified Frame within it. This may be obtained using the AST_GETFRAME function, as follows:
This would return a pointer (not a copy) to the base Frame within the FrameSet. Note the use of AST__BASE (§13.5) as shorthand for the value of the FrameSet’s Base attribute, which gives the base Frame’s index.
Removing a Frame from a FrameSet is straightforward and is performed using the AST_REMOVEFRAME routine. You identify the Frame you wish to remove in the usual way, by giving its index within the FrameSet. For example, the following would remove the Frame with index 1:
The only restriction is that you cannot remove the last remaining Frame because a FrameSet must always contain at least one Frame. When a Frame is removed, the Frames which follow it are re-numbered (i.e. their indices are reduced by one) so as to preserve the sequence of consecutive Frame indices. The FrameSet’s Nframe attribute is also decremented.
If appropriate, AST_REMOVEFRAME will modify the FrameSet’s Base and/or Current attributes so that they continue to identify the same Frames as previously. If either the base or current Frame is removed, however, the corresponding attribute will become un-set, so that it reverts to its default value (§13.4) and therefore identifies an alternative Frame.
Note that it is quite permissible to remove any Frame from a FrameSet, even although other Frames may appear to depend on it. For example, in Figure 14, if Frame 1 were removed, the correct relationship between Frames 2 and 3 would still be preserved, although they would be re-numbered as Frames 1 and 2.