An Experimental Alteration to the CUPID:FINDBACK Algorithm
An alternative form of the basic FINDBACK algorithm can be used by setting the (undocumented) parameter NEWALG to TRUE when running FINDBACK. The new algorithm is currently being assessed to see if it gives an improvement over the basic algorithm.
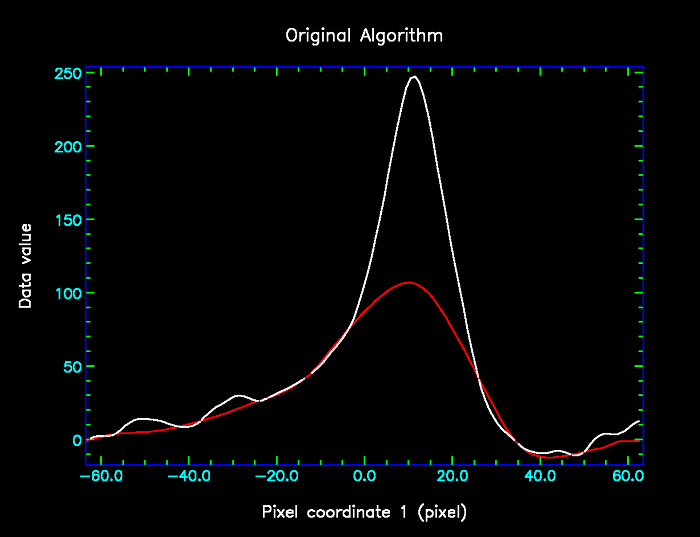
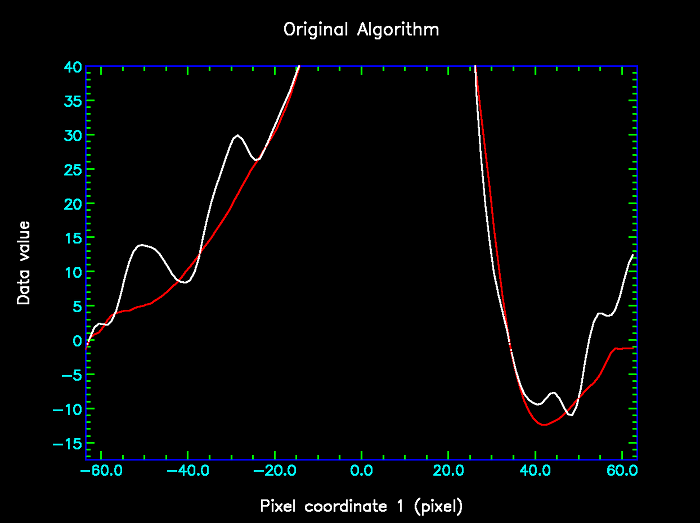
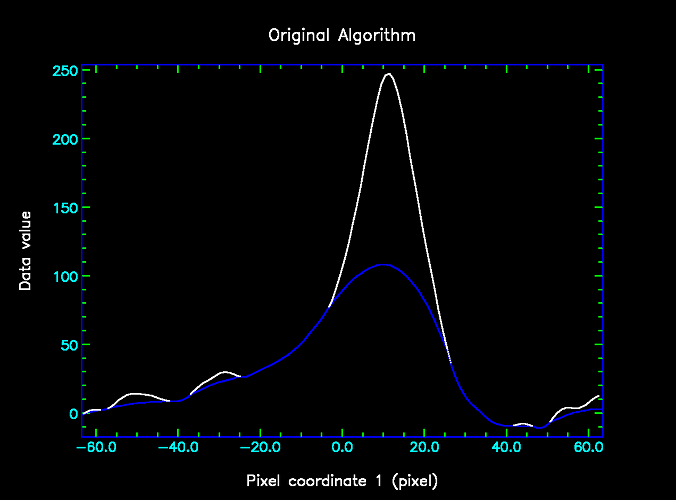
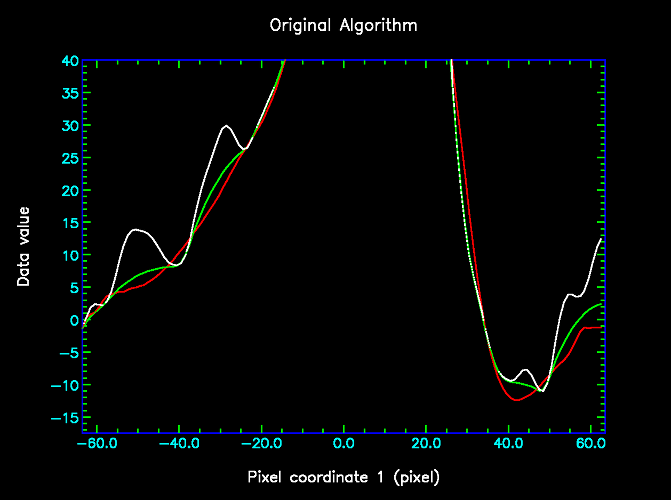
The problem addressed by the algorithm change is that, when processing high signal-to-noise data, the original algorithm can over-estimate the background in the vicinity of a narrow trough (more narrow than the box size). This is illustated in the following pair of images, in which the data is shown in white and the background estimate produced by the original algorithm (with box size 20 pixels) is shown in red. The right image shows the same data, but is restricted to the lower data values.
|
|
It can be seen that in places the red curve is higher than the white curve - most notably on the right hand limb of the peak, from pixel 25 and to 35. Whilst these differences may not seem very significant, compared to the other "wiggles", it should be remembered that this is low-noise data - the RMS noise was set to 0.01 when running findback implying that all the visible wiggles are believed to be real. In principle therefore, the red lower envelope curve should never pass visibly above the white curve.
In order to remove this effect, the new algorithm introduces a process that, effectively, modifies the background to be the lower of the background and the data curve.
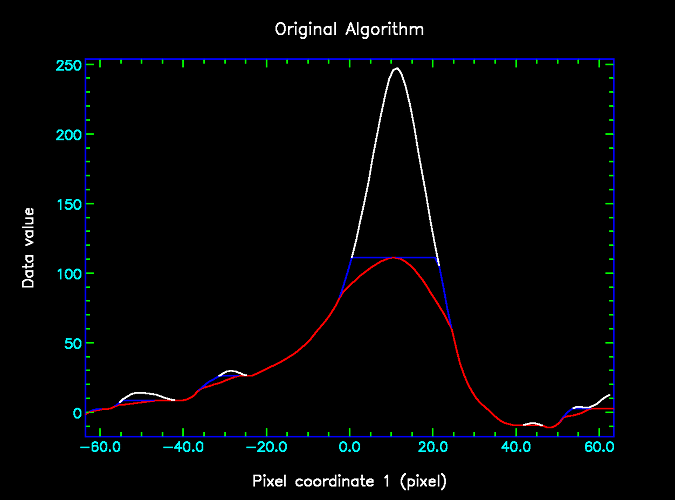
Specifically, the new algorithm differs from the standard algorithm in the way that the third filter is applied. To summarise the standard algorithm, it starts by filtering the data using a "minimum" filter followed by a "maximum" filter. This produces an initial estimate of the background, which is then filtered using a "mean" filter. The left hand figure below shows the result of the second (maximum) filter in blue, and the result of the third (mean) filter in green.
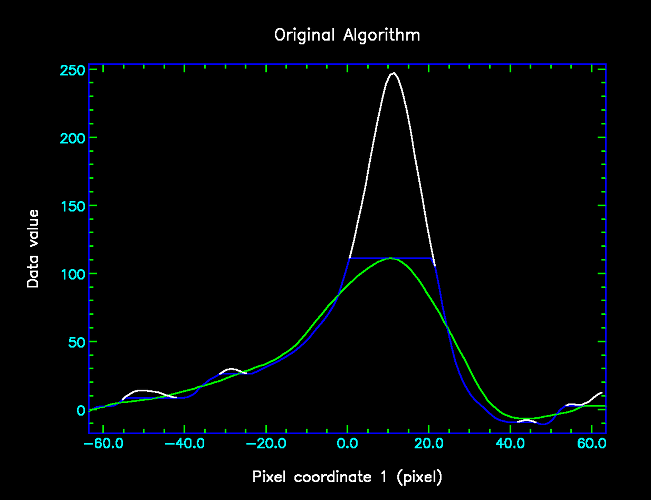
In the original algorithm, the green mean-filtered data is passed on to subsequent filters that attempt to correct the bias between the green and blue curves. In the modified algorithm, these subsequent filters are retained unchanged, but some extra steps are introduced before they are used, as follows:
1. Find the minimum of the original (blue) background estimate and the smoothed (green) background estimate at every point. This gives the red curve shown below.
2. Smooth the red curve with a mean filter, using a box half the size of the previous box. This gives the cyan curve shown below.
|
|
Whilst the cyan curve still pass above the white curve, it is a lot better than the green curve above. To achieve greater improvements, the new algorithm continues to iterate:
3. Find the minimum of the current smoothed (cyan) and unsmoothed (red) background estimates. This gives the blue curve shown below.
4. Smooth the blue curve with a mean filter, using a box half the size of the previous box. This gives the green curve shown below.
|
|
Again, it can be seen that the green curve is an improvement on the cyan curve above. This process of finding the minimum of the smoothed and unsmoothed background estimate, and then smoothing again with a half-sized box continues until the box size reached one pixel. At this point the loop stops, and the remaining (unchanged) filters are applied to remove any bias intoduced by the negative noise spikes.
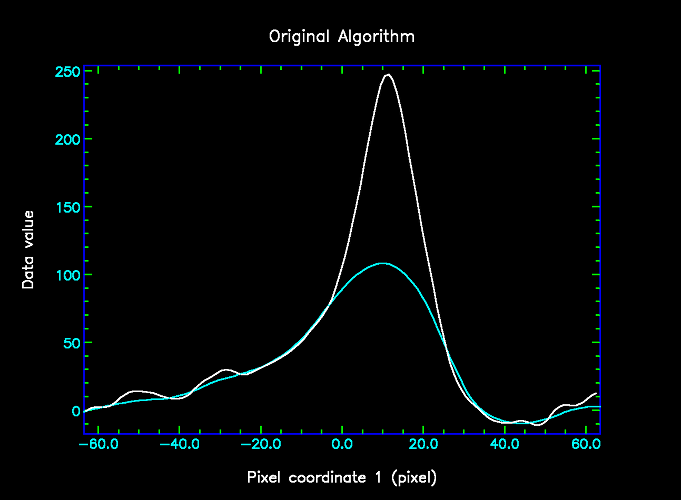
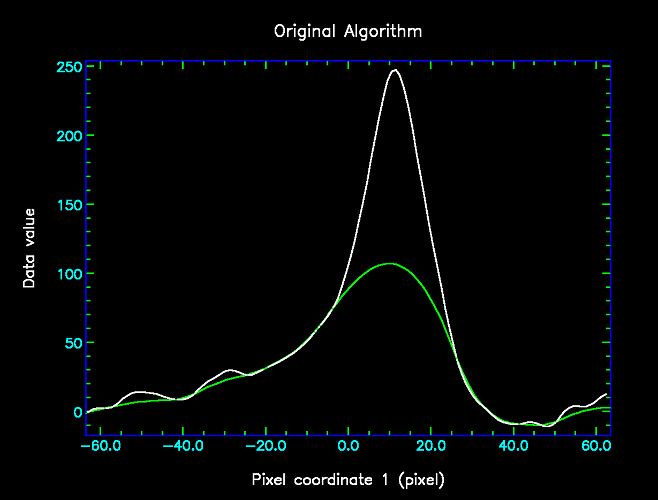
Finally, here are the first two figures again, this time with the result of the new algorithm shown in green.
|
|