4 Simple ESP Sessions

In this section a few example sessions are described as ‘blow-by-blow’ accounts.

4.1 Getting Help

The ESP help system is available from the UNIX shell like any other ESP command. To get help type:

If this does not generate a screen similar to:

then contact your system manager.

The help system is functionally similar to that found on DEC VAX machines. So replying to the query ‘Topic?’ with, for example, ‘loback’ generates another level of help:

4.2 Session 1 — Getting image statistics

An obvious example is determining the statistics (and in particular the modal count) of an image. So, imagine you are logged in and the esp command has already been issued, then the following session is what would be required to examine the NDF image p2 stored in the current directory.

At this point type in the file name, p2. The .SDF part of the name is not required. The application, in common with most ESP applications then gives you some useful information about the image in question. In particular, the image shape will give you some idea how long you will need to wait for you answers to appear.

You will find, as you use ESP applications more, that ESP applications will often volunteer a name for the IN file to be used. This name is shown at the end of the IN prompt between two ‘/’s. In this instance the suggested file name is galaxy. This name may be input immediately (if it is what you want) by pressing the Return/Enter key. On VAX systems, the current suggestion may be edited by pressing the tab key. You will find that many of the ESP applications will suggest answers to other prompts as well.

The application now prompts you for an indication of which image pixels are to be used in assessing the image pixel statistics. Frequently, you will want to use all of them, in which case your input should be ‘w’ or ‘W’. This application, and all other ESP applications, are not case sensitive so both responses are treated similarly.

If you are employing ARD files (see Appendix C ) to mask out bad pixels you should input ‘A’ or ‘a’. You will then be prompted for the name of the ARD file in question, in addition to those inputs shown below. It must be remembered that the name of the ARD file must be preceeded by ’ ̂’ or the input will be interpreted as a single ARD instruction and not a file name as intended.

If, instead you opt to use all the pixels, you enter ‘w’ in response to the USE prompt you will then be prompted as shown below with an appropriate response:

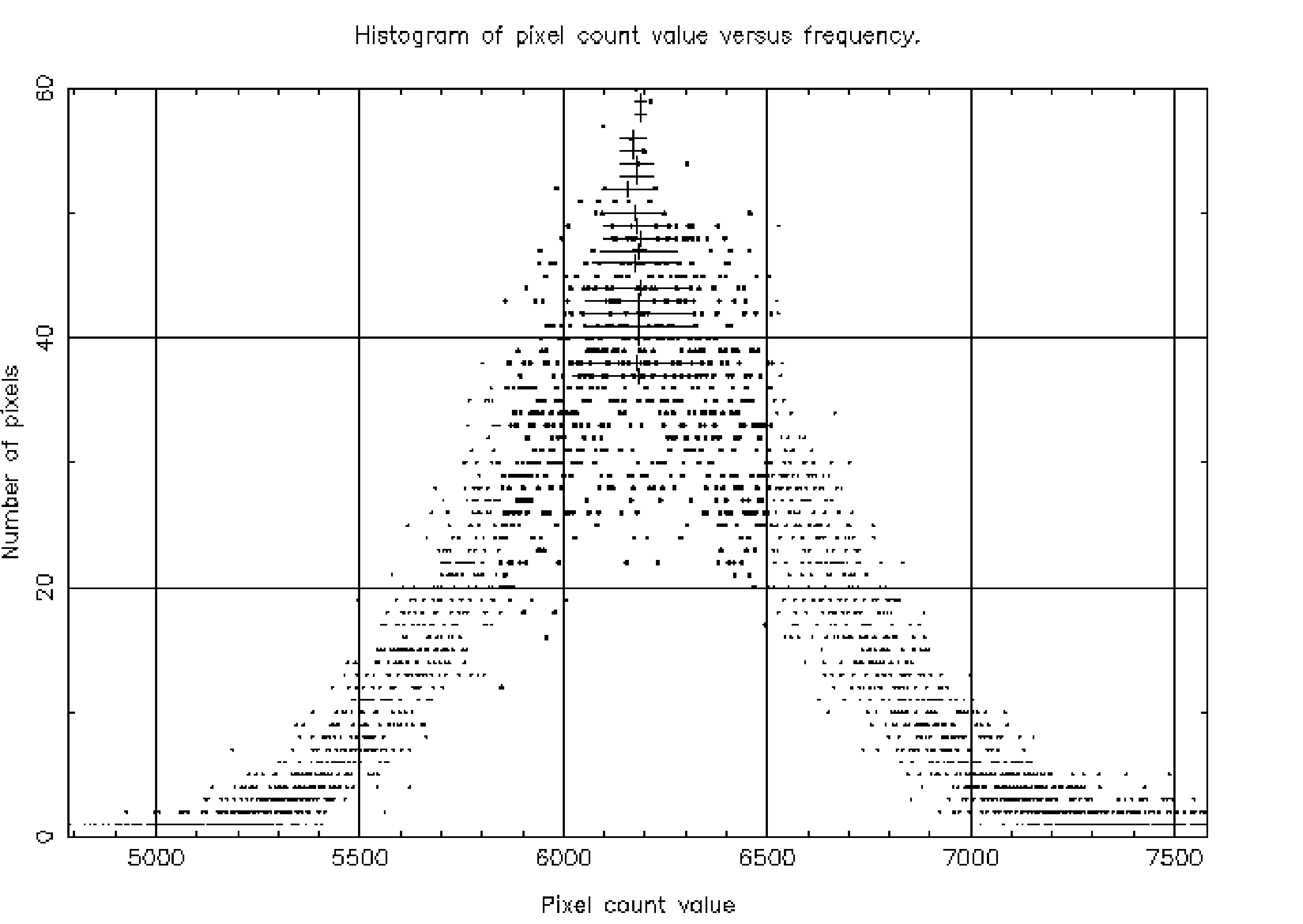
This simple set of instruction will then cause HISTPEAK to examine the NDF image p2 (a plate scan), using all its non-bad pixels. When a smoothed histogram is created by the application for determining a modal value (an unsmoothed histogram is always created as well) a Gaussian filter of radius 2 counts will be used. The histogram generated is displayed on device IKON. An example output display is shown as Figure 1 and the output to the screen is shown below.

Figure 1: The unsmoothed pixel count histogram generated by HISTPEAK.

If you re-run HISTPEAK but this time input an SFACT value of 4 you will find that the results for some quantities are different. This is as you would expect when histograms are smoothed. As you can see from the excerpt below, the values affected are those relating to values extracted from the smoothed histogram. Figure 2 shows the histogram and the effect of smoothing upon the shape of the pixel count distribution - smoothed points are plotted bold.

Figure 2: The smoothed pixel count histogram generated by HISTPEAK.

4.3 Session 2 — Interactive profiling by intensity analysis

One of the key uses of ESP is for profiling images of galaxies. The ESP application for doing this is ELLPRO. If we again assume we are logged on and that the esp command has been issued, then the following is a simple session using it. The example assumes also, that the kappa command has been issued allowing use of the DISPLAY routine. For the simplest use of ELLPRO, the image containing the galaxy to be profiled needs to be displayed.

The first instruction clears the X window and displays the NDF image file ic3374c. The second instruction defines the colour table to be employed for that window.

The next step is to start up ELLPRO and give it information about how you wish to work.

Choosing a value of TRUE for MODE tells the program that you will either be typing in a value for the location of the galaxy centre on the image or using a cursor to indicate where it is. The alternative is for the program to read in a list of co-ordinates from a text file. Specifying a value of TRUE for CURSOR then tells the program that you will be inputting the location by using a cursor. This is only possible if you have previously displayed an image on a device and it is still visible. If several images are currently displayed on a device then the most recently added image displayed (containing a DATA component) is examined. This information is obtained from the AGI database.

The next information required is the name of the display device on which your galaxy is currently displayed – in this case Xwindows. It then looks at the AGI database to determine what image you used to create the displayed image and displays its name to allow you to check that it is the right one. After a brief pause (duration depends on your hardware) the cursor may be used to identify the centre of the galaxy. How this may be done differs slightly from device type to device type. However, it is by use of buttons on an Xwindow and by use of the space bar and buttons on IKONs.

When you identify the location you want, the program reports that location in the Current co-ordinate system of the image, which in this case is SKY, with co-ordinates of RA and Dec. Information about co-ordinate systems associated with an NDF file is held in its WCS (World Co-oordinate System) component. Briefly, the WCS component contains several co-ordinate frames, allowing positions within the data array to be addressed in different ways. Each frame has a label, called its Domain, which usually describes the co-ordinate system; two important ones are GRID (which is always present) and SKY (which may or may not be). At any given time one of these frames is designated the Current one, and this determines the co-ordinates used when positions are requested or reported by ESP or other Starlink packages like KAPPA. You can change between frames using KAPPA’s WCSFRAME command. For instance the following would cause all positions to be reported in PIXEL co-ordinates instead:

To find out more about WCS components see SUN/95.

Once the galaxy centre is identified, it is necessary to describe how far out from the centre you want the profiling to continue (if possible). This is again achieved via the cursor.

When this has been done, a circle is drawn around the galaxy showing the extent of the profiling requested. This may, or may not, be visible depending on the colour of the image background. However, this can be overcome by use of the command line parameter COLOUR when starting ELLPRO, i.e.:

Where the valid range of colours (N) for drawing the lines is 0–3.

The next prompts displayed are simple to understand.

The first parameter, FRZORI, asks if the galaxy position you proposed (and refined with AUTOL if required) should be held to be the galaxy centre throughout the profiling operation or, is it allowed to vary slightly from ellipse to ellipse if that provides a better fit? BACK and SIGMA are the modal pixel value in the image and its associated standard deviation. Since the image in this example has a SKY co-ordinate frame (it does not have to be the Current frame), the program then works out the pixel size in arc seconds and reports it. If your image does not have any SKY co-ordinates, then you will be prompted to enter this as the value of a parameter PSIZE. The final group of configuration parameters is as follows:

ZEROP is the base of the scale for the surface brightness plot which will be made. AUTOL will refine the estimate of the galaxy centre position you have proposed with the cursor if set to TRUE. In the case shown it has been requested and the method chosen was a centroid. The last information required is to name an ARD file if one is to be used to define the good parts of the image. In this case ‘!’ is entered because no ARD file will be used. Instead, the whole image will be used. To make sure you’re aware of this, the program issues a warning.

It should be noted that for those required inputs which match the values suggested by the program, it is sufficient just to press the Return/Enter key to accept the proposed value.

The program then starts to work on the profiles. It first makes a guess at the crude shape of the galaxy at some smallish radius and (hopefully) sensible S/N ratio and displays this. Next, it makes a full estimate of the profile at that radius before dropping down to smaller radii and then increasing upward again until one of the profiling limits (see LIM1, LIM2 and RLIM in Appendix 0) is exceeded. Results of the profiling activity are displayed as they are calculated. This is done to allow you to see what progress is being made.

Descriptions for the headings may be found in Appendix F.

When the application has finished profiling the galaxy it issues a message indicating why the profiling action was stopped.

You are then prompted for the name of a device on which the image should be displayed. This is done by first asking you if the device currently displaying the image is to be used and then, if you say no, asking for the name of the new device. In the event that you request the current device as the place the profile results should be displayed, you will be further prompted to indicate (using the cursor) in which quadrant of the screen it is to be shown. It must be remembered that any objects in that part of the screen will, subsequently, be obscured, as may be seen in Figure 3.

Figure 3: The galaxy image and profile when displayed on the same device.

You are also prompted for the name of an output file into which the profiling results are to be placed. If it is found that the name you provide is not allowable (e.g. there are illegal characters in the name or the file named already exists) you will be reprompted. A ‘!’ may be used to avoid creating a file if you do not wish to retain a copy of the results.

Finally you will be asked if you wish to try again. If you answer yes, the program will go back to the point at which you identified the location of the galaxy centre on the image and start again. Where possible, you will not be reprompted for input you have already provided.

You will find that the ESP ELLFOU application works in a very similar manner. Consequently, you are now in a position to profile galaxies interactively and to generate profiles using either intensity (ELLPRO) or contour analysis (ELLFOU).

4.4 Session 3 — File based profiling by intensity analysis

Session 2 showed how one or more galaxies on an image might be processed interactively to yield their profiles. However, there are times when you want to profile virtually every object in an image. This can be done using ELLPRO or ELLFOU in essentially the same manner. The only difference is that you supply the image co-ordinates of the galaxies you want profiled in a text file. Such a file may be easily created using the LOGFILE option of KAPPA’s CURSOR or by taking information from a file generated by object identification software such as PISA.

The file used in the example below, contains the following:

The columns represent the $x$ and $y$ co-ordinates respectively. A third column might also have been included, giving a value for the background to be used for each of the galaxies. In the absence of a third column, the image’s global value is employed. Local background values for different points may be easily determined using the ESP LOBACK application.

The co-ordinates given in this file should be in the Current co-ordinate system of the image (which can be selected by WCSFRAME as described in the previous section), so that for instance if the image had the SKY frame as Current, a suitable file might read something like:

An example of the sort of input required is shown below.

Note that since the image in this example does not have a SKY frame in its World Coordinate System component, you have to enter the PSIZE parameter by hand.

In the example given, the co-ordinates file coords.dat identified the locations of 3 galaxies, but it could just as easily have contained information on many more. The current upper limit imposed by ESP is 10000.

4.5 Session 4 — Obtaining galaxy pieslice cross-section

The ESP application SECTOR may be used to interactively derive a pieslice cross-section of a galaxy. Before it may be used the NDF image containing the galaxy must be displayed on a suitable display device. This may be done in a manner similar to that described in Session 2. Once the image is displayed, SECTOR may be run.

The first prompt you are faced with asks if you are going to use a cursor to define the position of the galaxy centre and to describe the direction, size and length of the pieslice. If you answer FALSE to this query, you will have to input all your values via the keyboard. However, it is much simpler to use a cursor, as in the example below.

You are then asked on what device the image to be examined is displayed (DEVICE). SECTOR then examines the AGI image database to determine the image’s name. This is displayed so that the you can be sure the image used is as expected.

Control then passes to the cursor and you are prompted to use the cursor (and/or the keyboard) to identify the part of the image to be used in the pie-slice cross-section.

The application then asks for information about the image (BACK, SIGMA and, if necessary, PSIZE), how the results are to be displayed (SURF, RADISP, ZEROP) and where the results are to be displayed (SAME, DEVICE).

The RADISP and SURF options above specify that the ‘profile’ will be displayed in the form of surface brightness versus linear radius. Other options exist for displaying the mean pixel count versus radius transformed into its logarithm, square root or quarter power.

AUTOL set to TRUE means that the application will look at the parts of the image immediately surrounding the galaxy centre suggested and, if possible, will identify a better candidate. In the instance given AUTOL has been used.

The option MIRROR allows for the pieslice defined to be duplicated on the other side of the galaxy origin. This effectively increases the signal since more of the image will be sampled, but is only really applicable when the image is roughly symmetrical. Figure 4 shows the selected sector displayed on the galaxy. It also shows the mirror image sector generated by the MIRROR parameter being set to TRUE.

The graph is then displayed and you are asked to indicate (using the cursor) the radius range of the profile points to be used to calculate the scale lengths.

The graph then displays the galaxy profile ‘fits’ and the results of the scale length calculations are printed, showing values for the central surface brightness of the galaxy for both elliptical and spiral galaxy models.

Figure 4: The galaxy image, showing the sector area sampled and profile.

Finally, you are given the chance to obtain a pieslice of some other part of the image.

4.6 Session 5 — Examining profiling results

The applications ELLPRO, ELLFOU and SECTOR all generate text output files that may be examined using the application GRAPHS. This lets you display graphs such as surface brightness, ellipticity or position angle versus radius (or some transformation thereof). GRAPHS has been made as simple to use as possible. A simple session is shown below. The input file used (prof.dat) was generated by ELLPRO.

By opting for MODE to be TRUE, you have opted to interactively examine each of the profiles from the input file in turn. In this mode, the profiles are displayed (if required) on a graphics device and you must identify the radius range of the data points to be used to determine the galaxy scale length. CURSOR set to FALSE means that the radius range will either be typed in or GRAPHS will automatically guess at an appropriate range to use. The inputs INFILE and OUT identify the input and output text files respectively. The graphical output is shown in Figure 5.

Figure 5: The galaxy profile with elliptical and spiral models shown.

GRAPHS shows you the name of the application that generated the profile you are examining and the name of the image from which it was derived. It then asks you to define what is to be displayed. WHATD set to ‘s’ means surface brightness will be displayed against linear radius (defined by RADISP set to ‘r’). DEVICE again defines the name of the graphics device to be employed while RRANGE and FITLIM define the radius range of the part of the profile to be fitted.

Two sets of co-ordinates are displayed here to identify the point in question: those of the Base frame (GRID co-ordinates, which always start at (1,1) for the bottom left pixel in the image) and those of whatever was the Current frame when the file being plotted by GRAPHS was generated. If the Current co-ordinate frame of the image has been changed using WCSFRAME then the Current co-ordinates will no longer be correct, but the Base frame ones always will. You can set the Base frame to be Current, and so used for display etc., at any time by doing

More information is then given; values for central surface brightness (CSB), scale length and range of data points used are displayed. The LCC (linear correlation coefficient) values give an idea of how good the fit was. Finally, you are given the option to try fitting the profile again. If there is only one object in the input file, the application will then stop, otherwise the next profile from the file will be read and you will be allowed to profile that.

One detail of this example needs a little more explanation. In one of its modes, GRAPHS can work automatically on input files containing information on lots of galaxies without further input. This means that GRAPHS can take the file generated in Session 3 (containing the profiles of three galaxies) and determine from them, values for the central surface brightness and scale length. This method of working is selected by setting MODE to FALSE, but otherwise differs only slightly from the example above.

4.7 Session 6 — Looking at the image background variation

In this session, the ESP application SKEW is employed to show what parts of a source image suffer from poor flat fielding. Before you run this program you should run HISTPEAK for the source image to determine its background value and also its associated standard deviation.

Then, the session will go something like this:

The parameters IN and OUT refer to the source image and the output image respectively. BACK, SIGMA and PSIZE all relate to the image cnt4141c.

When the MODET option is set to FALSE, SKEW calculates a local background value when determining the skewness of each part of the image. In this example it is set to TRUE, so the image’s global background value is used instead. This is the faster option.

USEALL and NSIGMA are used to define a pixel count cutoff value. If one of the image pixels is brighter than the global background (BACK) plus a certain number (NSIGMA) of background value standard deviations (SIGMA) it is excluded from the calculations. This may be used to reduce the influence of cosmic rays and other bright image features which might otherwise dominate the output.

Since skewness values are usually fairly small, a multiplying factor may be applied to all the skewness values calculated. This is specified by MULT.

Finally, SKEW shows you what it is currently doing and how far it has got. This is because, for large images, it can take a considerable time to run, especially, if the template size is large.

Figure 6 shows a source image and the image generated by SKEW when it was sampled over boxes approximately 10x10 pixels in size. Note how the previously unnoticed bad column (slightly left of centre near the top) is easily spotted and how large the full extent of the poor flatfielding is.

Figure 6: A poorly flatfielded source image and the output generated by SKEW.

4.8 Session 7 — Interactively obtaining 2-D Gaussian source profiles

In some of the earlier sessions you saw how to profile a galaxy in terms of an ellipse using ELLPRO and ELLFOU. Sometimes in astronomy it is useful to profile a source (or sources) in terms of 2-D Gaussian functions, this is especially useful for users of JCMT data (see also JCMTDR). In ESP this operation is performed by the application GAUFIT.

GAUFIT is similar to ELLPRO, SECTOR and ELLFOU in that it may be operated using a cursor or a simple text file to select the source position(s) that must be examined.

GAUFIT now contains two distinct fitting algorithms: the original one, which obtained the fit parameters by hunting through a region of parameter space constrained by you, and a new one (as of version 0.9), which uses a non-linear least-squares algorithm to obtain the parameters and their uncertainties. For further details on the new algorithm, see the detailed description of GAUFIT in section 0. The interface has not changed radically, but I will show two complete examples below.

4.8.1 GAUFIT: original fitting algorithm

Once the image to be analysed has been examined using HISTPEAK and displayed using KAPPA’s DISPLAY, an interactive session might proceed as follows:

You can choose several sources to fit. We chose to fit only one here, so quit at this point.

This is very similar to the way in which ELLPRO, ELLFOU and SECTOR works. After first defining the colour (COLOUR) of the ink to be used to mark the image locations specified, the angle convention to be used is defined (via ANGCON and ANGOFF) and then the device displaying the source image chosen (IMGDEV).

If you set FWHM to be true, then results will be displayed as FWHM, rather than the gaussian width parameter, sigma.

If you set the parameter LSQFIT to be false, you get the original GAUFIT algorithm.

It is then necessary to provide information on the image background value (BACK) and its standard deviation (SDEV). These are most easily found using ESP’s HISTPEAK. For most purposes the interpolated standard deviation is best.

The parameter NSIGMA defines a count value (NSIGMA times the SDEV value plus BACK value supplied) above which a pixel must be for it to be included during the minimisation process. This is to reduce the number of pixels considered and avoid ‘noisy’ pixels contributing. Using too low a value will slow the application down a lot. ITER merely tells it how many minimisation loops must occur before the processing stops. As with all minimisation processes the application can reach the ‘point of vanishing returns’ if too many iteration loops are specified. The arbitrary residual indicator will be a useful help. See below.

The parameter MODEL is the name you wish to give to the output image while MODTYP defines what sort of image it should be. There are two options: the first is a whole image (MODTYP=W) where the model value for every pixel of the image is calculated, the second (MODTYP=R) where only the areas of the image immediately surrounding the sources are shown as non-bad. In these regions the residual value is given (ie the source image value for a given pixel minus the model value for the same pixel).

These parameters define how tightly constrained the minimisation routine is when it tries to walk through variable space. That is, if any of these values is very small (say .001) the minimisation can only adjust that aspect of the source model very slightly. The other extreme, a lot of freedom to vary source parameters, is specified if the value supplied is 1. So in the case shown above, the centres of the source cannot be varied much (XINC and YINC), while the breadths of the sources, peak height and position angle (SAINC, SBINC, PINC and ANGINC respectively) are allowed a lot of freedom to vary. The ability to constrain an aspect for the source model is essential for merged sources.

Setting AUTOL true means that the application will try to improve slightly on the source positions you have suggested using a centroiding routine. This is particularly useful with very large images where the display window you are using may not be able to provide a 1:1 relationship between the pixels in the image and the pixels on the screen.

As you can see, the source positions remained unchanged during the minimisation (as requested by the small values we assigned for XINC and YINC) while the other parameters varied considerably – note that even at the last iteration the position angle of the source is still varying and the residual is dropping. The X and Y co-ordinates reported here, and those written to the output file ic3374c-txt, are in the Base co-ordinate system of the image.

An example output file is shown in Section 15 and described in Appendix F.

4.8.2 GAUFIT: least-square fits

Fitting with the least-squares algorithm proceeds much as before:

So far, the interaction with GAUFIT is exactly as before, but now we choose to use the new algorithm.

You choose to use the new algorithm by setting the parameter LSQFIT to true. Around half of the function-evaluations in the fitting algorithm are used to calculate the uncertainties in the fit parameters, so if you have no need for these (for some reason), you will save a significant amount of run time by not requesting them.

This algorithm can fit the background count, so you do not need to use another routine to determine this. If you do give a positive value for the BACK parameter, then the routine will use that instead of fitting it (there is absolutely no speed advantage to this).

Unless you suspect the algorithm is somehow misbehaving, you should not give a positive value for the iteration count: the default is 150, and the fit should converge well before that, so that this parameter merely acts as a check on any pathological cases which cause the routine to somehow run away with itself.

For the LSQ algorithm, there is a third option for MODTYP. MODTYP=G gives a ‘regression diagnostic’, which is an image in which the value at each point is the change in the residual function if the corresponding point in the data were deleted. The residual function is half the sum of the squares of the differences between the model and the data. This is expensive to create, so you should not select it unless you actually wish to examine it.

There is a good deal of information in the text which GAUFIT produces while it is working.

For each iteration, GAUFIT prints the number of function evaluations so far, the ‘drift’ from the initial guessed position, and a residual. The ‘drift’ is a scaled estimate of how far the current solution $\left(x,y,{\sigma }_a,{\sigma }_b,\theta \right)$ is from the initial one, with the different components of the solution appropriately weighted. If the drift reaches 1, the routine will conclude that it has somehow got lost, and give up with an error message to that effect. The scale for this calculation is set when you ‘Indicate the outer limit of the source’ at the time you pick the source positions – you might want to select a small circle if there are several sources which might become confused with each other. The ‘normalised residual’ is related to how much the model deviates from the data, but the numerical value is unimportant – it should decrease as the calculation goes on.

When the routine calculates the parameter uncertainties, it assumes a value for the data standard deviation based on the size of the residual and the number of parameters and data points, and it reports this for your information. If this value seems unreasonable, because it is substantially different from an alternative estimate you have of the standard deviation, please let me know.¹

The routine also reports an estimated condition number (the ratio between the highest and lowest eigenvalues) for the Hessian used in the uncertainty calculation. If this is huge (more than about $10^6$), you should not place too much reliance on the uncertainties produced. In this case, the condition number is larger than we’d like, but the reported uncertainties should not be too far out. A condition number less than $10^3$ would suggest good reliable uncertainties.

In adapting the least-squares algorithm for this particular application, I made one or two optimisations, and the ‘optimisation metric’ indicates how well this is performing. It’s scaled so that a value towards 1 indicates that the optimisation is working as expected, zero means I needn’t have bothered, and negative values suggest it’s actually creating more work than the unimproved case. If you have a non-pathological case which gives negative values here, I’d like to hear about it.

Finally, the routine reports that it has converged successfully (if it hasn’t, it should give a more-or-less useful explanation here).

The routine displays its results, then their corresponding uncertainties, with negative uncertainties indicating that no estimate was made. The routine does not (in this release) make an estimate of the peak flux uncertainty.