6 Scan maps

Scan maps, i.e. mapping while continuously scanning the array over the source, require a few additional steps in the reduction procedure. The reduction process is also different depending on whether we made conventional scan maps or used the “Emerson2” technique. Conventional scan maps refer to maps done while chopping in the scan direction and restoring the resulting dual beam map with the EKH algorithm (the Emerson-Klein-Haslam algorithm – known to all who have ever used nod2 or JCMTdr [7]) before transforming the map into equatorial coordinates. The “Emerson2” technique is essentially a basket weaving technique, where one can scan in an arbitrary angle but chop in two orthogonal directions and restore the dual beam map in the Fourier plane after converting the dual beam maps to equatorial coordinates. This method therefore requires a minimum of two maps, one where we chop in RA and one where we chop in Dec. The standard setup for SCUBA is to use six maps, three of which are done while chopping in RA with chop throws of 30, 44 and 68”, and three while chopping in Dec with the same three chop throws. The chop throws are chosen so that we should be sensitive to most spatial frequencies in the map. If possible one should try to choose the map size so that it covers the whole source and provides an additional baseline region off source, but as we all know this is not always possible.

For all scan maps we can do the first three reduction steps: reduce_switch, flatfield, and extinction, the same way as we would do for any jiggle map. We also blank out noisy bolometers, but from here onwards we need to apply slightly different methods. Scan maps are also affected by sky noise, especially when we use the “Emerson2” technique. This is because the time difference between when the positive and the negative beam passes the same position on the sky can be significant, and sometimes even longer than in jiggle-maps. This is especially noticeable for large maps and large chop throws. We can crudely remove sky noise in scan maps, but not as well as in jiggle maps, calcsky is our main tool and needs several repeats of the same maps to work efficiently.

6.1 Despiking

After we have extinction corrected the map and taken out noisy bolometers, we need to despike the data. This is done with the Surf task despike2, which takes a small portion from each end of a scan and computes the rms–variations for each bolometer and then does a standard sigma clip. If you want to be conservative, use 4 sigma. This does a reasonable job, but large spikes (extending over several seconds in time) are not detected and these will have to be removed manually using sclean or dspbol. It is often necessary to run despike2 a second time after scan_rlb, because even with the same sigma threshold, the rms is now smaller and one finds a fair amount of residual spikes missed in the first round.

6.2 Base line removal - scan_rlb

The SCUBA on-line software normalizes each scan in conventional (EKH) scan maps, which leads to baseline offsets, but even the “Emerson 2” maps have baseline uncertainties. Spillover, large spikes and sky noise add to these baseline uncertainties. It is therefore absolutely necessary to remove the baseline offset for each bolometer. If it is omitted one may end up with severe striping in the map. If your map is large enough, i.e. you have no source emission at the end of your scan, you can run scan_rlb, and fit a linear baseline for each scan (exposure and bolometer) by taking the end portions of the scan as a measure of the signal level. The default size of the region used for the baseline subtraction is the number of data points in one chop throw. This can be inadequate for the small chops, especially if the data are spiky or suffer from sky noise variations, and you may consider increasing the default to perhaps 100”. The output from scan_rlb is the basic map name, now appended by _rlb, which is the file you will use as an input for the next stage in the data reduction.

However, if your map is not large enough to start and end on a region free of emission scan_rlb will result in a gradient over the scan. Taking the default behavior of scan_rlb in this situation is probably the leading cause of poor results obtained from scan mapping. When you map galactic regions it is usually better to use the median rather than the default, which is linear. Another, sometimes more successful approach is to use SCUBA sections.

In scan map mode each ‘sweep’ or ‘raster’ is a section (exposure), and the complete map is an integration. If you believe that you have sections of the map that are free of emission, you may be in luck, and you can use these emission free sections to provide the baseline level for the rest of your map. To find out which section is which, display your rebinned map and then use scuover. To produce the image in Fig. 8 we typed:

One can see that the scan map started at the top right of the map (a scan map of the moon’s limb) and took 11 ‘sweeps’ or exposures to complete the map. One can see that only exposures 1, 9, 10 and 11 started and ended off source. Therefore when one wishes to remove the baselines (remembering that one now has to go back 2 or 3 steps to do this) from this image the best method would be:

Its obvious with a source like the moon when you are on and off source and because the moon fills most of the image, the data were additionally masked. This is a rather special case, where it would have been very difficult to do the baseline subtraction any other way without ending up writing special purpose software. For molecular clouds and star forming regions it is often very difficult to find emission free regions. For really extended emission, like the Galactic center, it was therefore found that the best way to do baseline removal is to use the median level of all the scans for each bolometer (Pierce-Price et al. [15]), which corresponds to specifying SECTION as {}. Quite often you will find that you have to do an initial map reduction to see how extended the region is and where you can find emission free areas. Once you know this, it is much easier to go back to noisy sub-maps and redo the baselines.

Figure 8: An example of a scanmap of the moon’s limb. The SCUBA array’s position at the beginning of the observation is shown. In total it took 11 ‘sweeps’ or exposures to map the area requested.

6.3 Sky noise removal in scan maps

There are no sky bolometers in a scan map, i.e. each bolometer can be on source, and furthermore a bolometer will cover a different region of the sky for each map exposure. It is therefore not possible to remove sky noise the way we usually do for jiggle maps. Sky noise can be extremely severe and rapid on Mauna Kea. Under such circumstances sky noise variations can completely distort a scan map, especially for large chop throws. calcsky was originally developed to give us a technique for reducing sky noise in scan maps, but as we have seen it works also quite well for jiggle maps, as discussed in Section 5.5. calcsky computes a model of the source emission, and subtracts it from the data for all bolometers as a function of time. Several maps can be co-added.

Below we test calcsky on a small scan map, taken with a 20” chop in RA. The map file, rn14_lon_dsp has already been baseline subtracted, pointing corrected, calibrated and despiked.

We can now examine the sky variations with linplot. There seems to be clear systematic variations as a function of time, but the maximum deviation is only $\sim$ 150 mJy/beam, c.f. the jiggle map we did earlier (Fig. 5), which showed sky noise variations of about 600 mJy/beam.

However, we can easily check how much we gain in noise performance if we remove the sky noise from the data. We therefore run remsky on the same data file that we processed with calcsky.

In this case the gain was rather marginal. The despiked data file gave an rms noise of 70 mJy/beam after running it through rebin while the sky corrected one improved by $\sim$ 0.5 mJy/beam (i.e. an improvement of less than one percent), when examined over the same area of the map, which means that it was not really worth doing. Nevertheless, I go through all six maps in the set, and find as I had expected the largest sky fluctuations for maps taken with a 65” chop throw. In the last map of the set (65” chop in Dec), the maximum sky fluctuations were $\sim$ 250 mJy/beam, or peak–to–peak sky noise variations of $\sim$ 500 mJy/beam, resulting in a 7% improvement in noise after subtracting the calculated sky noise variations.

calcsky does not work very well on a single map, but since calcsky can account for the chop throw, one can use a first version of the final map as a model for the individual sub–maps. If necessary, one can do a second iteration by using the sky corrected sub–maps to create a new improved map, which can be used as an even better model for calcsky.

From here onwards the rest of the reduction differs depending on the scan map mode.

6.4 Conventional scan maps

After we calibrated the maps and done the baseline removal, we need to restore the map from a dual to a single beam map. This is done by using restore. This task does a standard EKH restoration. Below we show an example of restoring a scan map of NGC 7538, a high mass star forming region. In this case we accept the default for the chop throw, but if the restored map looks poor, it is most likely because the chop throw deviates from the nominal value.

Once this is done, we can apply pointing corrections to remove any pointing drifts we had during the duration of the map. If the map is still uncalibrated (we strongly recommend to apply calibration immediately after the extinction correction), we should do it now. Once we have all the maps calibrated we can proceed and co-add any additional maps that we may have using rebin, exactly like we do for jiggle maps. Note that if you co-add data sets taken in different weather conditions or during different nights, you will have to weight the individual data sets in order to minimize the noise in your final map.

6.5 Scan maps taken with the “Emerson2” technique

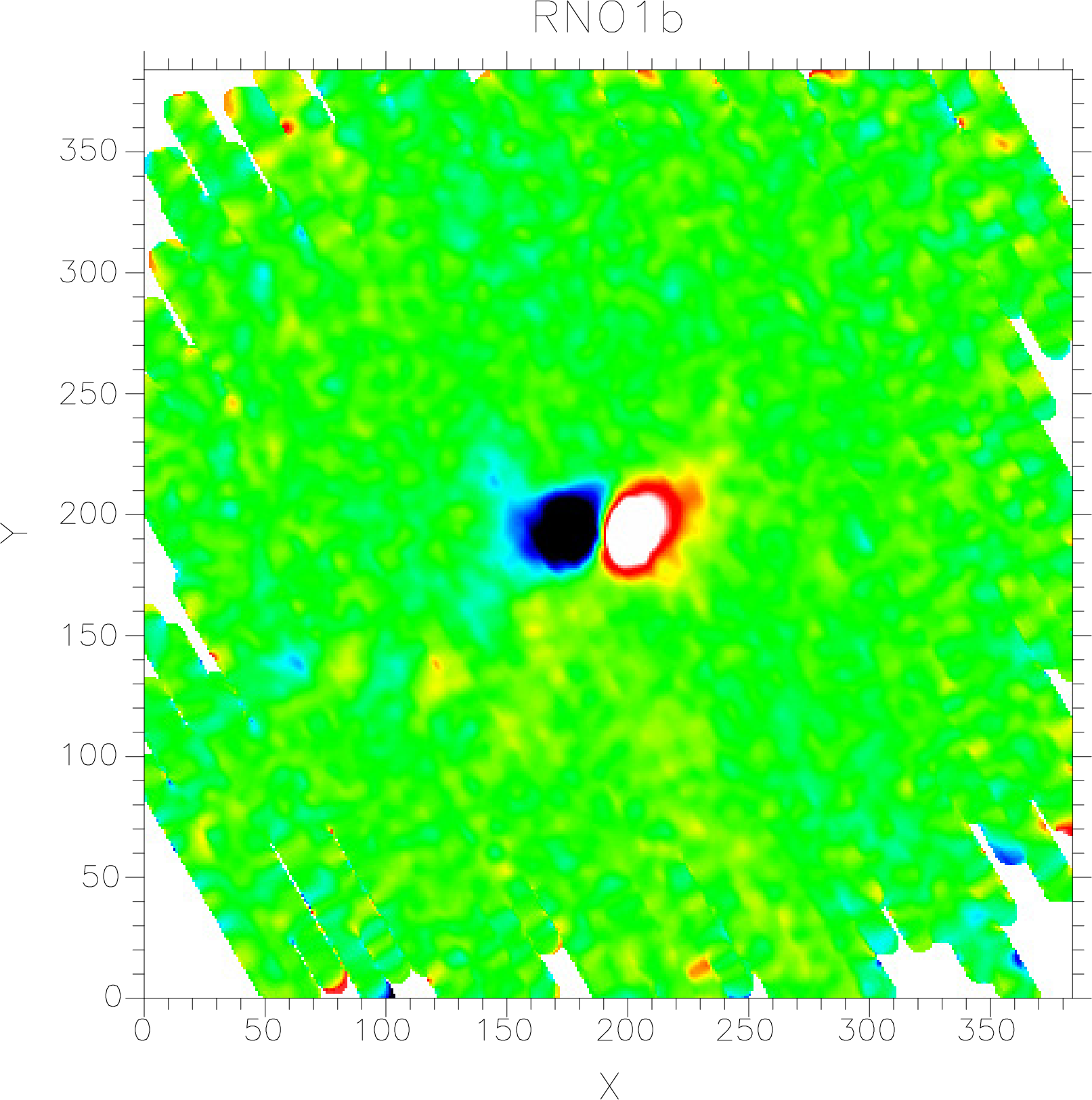
Scan maps taken with the “Emerson2” technique, i.e. basket weaving in Fourier space, have to be run through rebin without restoring them from dual to single beam maps and in the same coordinate system that was used for the chop throw (e.g. RJ or PL). You have to make one map for each chop throw and each map has to have identical dimensions and pixel size. We recommend that you make the maps larger than the area mapped and then cut them in size after running them through remdbm, the final reduction stage for “Emerson2” scan maps. Since remdbm makes use of fast Fourier transforms, it is advisable to choose map sizes, which are a power of two. Make sure that you do not choose a size equal to the default size for any of the sub–maps, because in that case rebin will choose its own map center, which is not equal to the center pixel of the map. The end result will be a garbled map. To make it easy to identify the map sets we need for remdbm one can give the calibrated, noise weighted and co-added maps names like : m30ra.sdf, m44ra.sdf, m30dec.sdf, m44dec.sdf etc., not because the tasks need it, but it easier for book keeping purposes. These maps also have to be corrected for pointing drifts but they should not be restored. The maps are still dual beam maps and each source in the map should show up as a positive and a negative feature in the image. Fig. 9 shows the first sub–map of RNO1b, i.e. scan rn14_lon_sky, which we used to test calcsky in Section 6.3. It has now run through rebin and given a size 384 $\times$ 384 with a pixel size of 1”. Since this map was taken with a 20” chop in RA, we called it ra20.sdf . We should have made the map slightly bigger, because the maps with 30” and 65” chops will cover a larger area. Note that this map was taken at a time when the recommended chop throws were 20”, 30”, and 65”, now the recommended minimum set is 30”, 44” and 68”, which gives a somewhat better recovery of spatial frequencies.

Figure 9: An example of the first map in a series of 6 maps taken with the “Emerson2” mapping technique. This is a calibrated map with a 20" chop in RA, which is converted to RJ with rebin but still unrestored. We can see the positive and the negative features in the map, and a few noise spikes at the edges of the map.

Once we have all maps pointing corrected and co-added to the same pixel size and dimension, we can run remdbm which converts the maps into our final image. In the example below I take the six sub–maps of RNO1b and convert them into a map called rno1b_lon_reb using remdbm. We specify the name of the final map with the parameter out, and a provide the task with a listing of the files, see below:

remdbm also accepts wild–cards and we could therefore have listed the files as ra* dec* and it would have picked up the whole set of six maps. Neither do we have to give it chop throw or chop direction. It will extract that information from the FITS–header. The task can restore a single map file, but even two maps in orthogonal directions looks rather ugly, and it is strongly recommended to use a set of 4 or 6 maps.

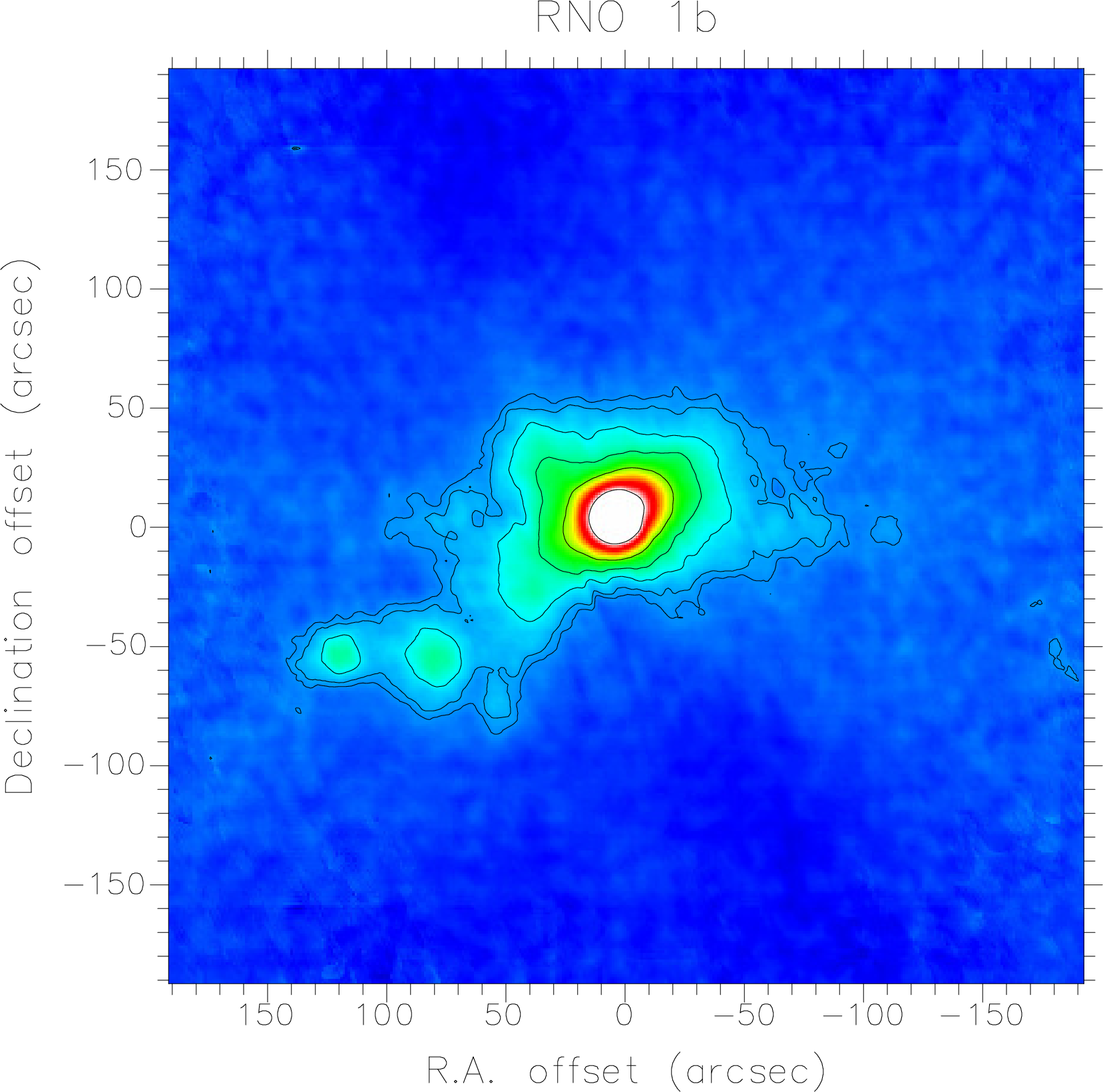
Due to the way the Fourier transformations are done, remdbm forces the sum of all pixels to be zero. This will introduce a small negative background level in the map. We can remove this baseline by analyzing the map with Kappa’s stats or with Gaia and add back the level we deduce with cadd. For our map we find the negative baseline to be $\sim$ 0.3 Jy/beam, which we add to the map. The final, baseline subtracted map is shown in Fig. 10.

Figure 10: Our final “Emerson2” scan maps of RNO 1b. The map has a little bit of negative residuals in the scans that went over the strongest part of the map (edge of the map at p.a. $\sim$ 30 and 210 degrees), indicating that the baseline removal was not perfect, but it does not show up with the contrast used for this figure. For a published version of the map, see Sandell and Weintraub [16].